The Fourier Transform NMR Experiment
Although most of you have been introduced to NMR spectroscopy in your organic chemistry courses, this introduction will start with some basic principles of NMR and then explain how these principles result in the observed spectra. Even so, it would be helpful to review your organic chemistry text before reading this introduction.
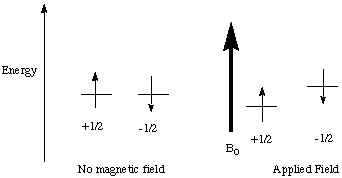
A nucleus must have a non-zero nuclear spin (I) to be observed in an NMR experiment. The most commonly observed nuclei have I=1/2 (1H, 13C, 19F, 31P). The nuclear spin, although not really a physical "spinning" (this is in the quantum mechanics realm) has an associated magnetic moment vector that will interact with a magnetic field (just like a spinning charge in classical mechanics). The nucleus has spin states I, I-1, ..-I available. In the absence of a magnetic field, all of these spin states are degenerate. This degeneracy is removed when a magnetic field, B0, is applied (See Figure 1). The lowest energy state has the spin magnetic vector aligned parallel to the magnetic field. In the higher energy state, the vector is aligned antiparallel.

Figure 1.
The splitting due to B0 is dependent on the magnetic field strength according to equation 1, where gamma is a constant called the magnetogyric ratio (which varies from nucleus to nucleus), h-bar is Plank's constant divided by 2pi, and B0 is the strength of the applied field. The energy splitting induced by the magnetic field is not very large. By applying Boltzmann's Law, it is found that the excess nuclei in the lower state for a 7 tesla magnet at 293 K is only 0.005%.
![]() (1)
(1)
Absorption of Radiation
Just as with electronic and vibrational spectroscopy, the nuclei can be promoted to higher energy states by the absoption of radiation. When the energy of the radiation matches the energy difference between the spin states an absorption of the photon takes corresponding to the change in spin state (Figure 2).
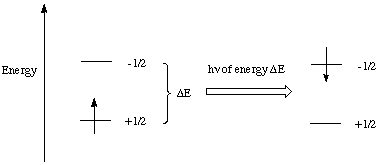
Figure 2. Nuclear spin state change induced by radiowaves.
What makes NMR so useful as a tool for structure determination is the varying chemical shifts. The frequency of absorption for a nucleus depends on its chemical environment. The other nuclei and electrons in the molecule shield the nuclei from some of the magnetic field so the effective magnetic field felt at the nucleus is somewhat less than the applied field. If all nuclei or even all nuclei of the same type (i.e. 1H) absorbed at the same frequency, the usefulness of NMR would be greatly diminished.
The positions of the peaks in an NMR spectrum are reported in parts per million (ppm). the frequencies actually detected by the instrument are in Hz, but as can be seen from equation 1, the frequency of a transition is dependent on the field strength of the magnet used. Since the frequency detected is proportional to the field strength, a chemical shift scale, independent of field strength can be easily constructed. The chemical shift, delta, is defined as
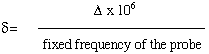 (2)
(2)
where delta is the difference between the peak and a reference peak (in HZ). The probe frequency is in units of MHz and delta is in units of Hz, so a factor of 10 6 is required. Chemical shifts therefore have units of ppm.
Some rules about chemical shifts are as follows
·Nulcei in different chemical environments absorb radiation of different frequencies
(barring coincidence)
·Nuclei in the same chemical environment absorb radiation at the same frequency
(chemical shift equivalency)
Some examples are given below
· In CH3Cl, there are 3 H's in the same environment so all are chemical shift
equivalent and result
in a 1H NMR spectrum with a single peak
· In methyl acetate, the protons in the methyl group B are in a very different
environment than the
protons in methyl group A so the two methyl groups have quite different chemical
shifts (they are chemical shift inequivalent)
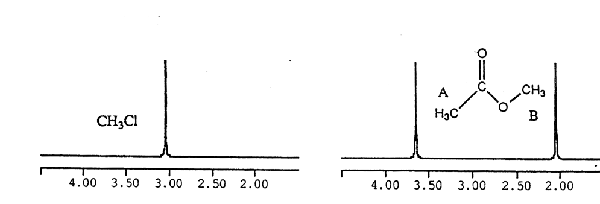
Figure 3. NMR spectra of chloroform and methyl acetate.
You might also realize that the three protons on each of the methyl groups in methyl acetate do not have the same environment because they are oriented differently with respect to the carbonyl group. Despite this fact, the 1H NMR spectrum of this compound has only two resonances, one for the protons on methyl group A, and one for the protons on methyl group B. The methyl groups are rotating rapidly, and as a result the average environment of these nuclei is observed in the NMR spectrum.
Up to this point, the examples considered contain sets of spins that give rise to a single line in the NMR spectrum. The chemical shift of these singlets is determined by the local chemical environment that influences the magnetic field about the nucleus. Other nearby spin-active nuclei, (nuclei having non-zero nuclear spin), also affect the local magnetic field about a nucleus. This phenomenon, referred to as coupling, leads to additional splitting of the resonances for groups of coupled nuclei. Coupling is transmitted by the valence electrons of a molecule. The magnitude of the coupling is related to the number of bonds separating the coupled nuclei. Coupling between nuclei separated by four or more bonds is not generally observed.
For two I = 1/2 nuclei coupled to each other (call one A, the other is X), there are two different possible orientations of the magnetic moments for both the X and A nuclei. The energy of the X transition depends on the spin-state of the A nucleus to which it is coupled; likewise, the energy of the A transition depends on the spin state of the X nucleus to which it is coupled. Accordingly, the signals for both the A and X nuclei appear as two lines, equally displaced above and below the respective frequency for the uncoupled nucleus (see Figure 4). The splitting between these lines (usually expressed in Hz, NOT ppm) is referred to as the coupling between A and X and is denoted as JAX
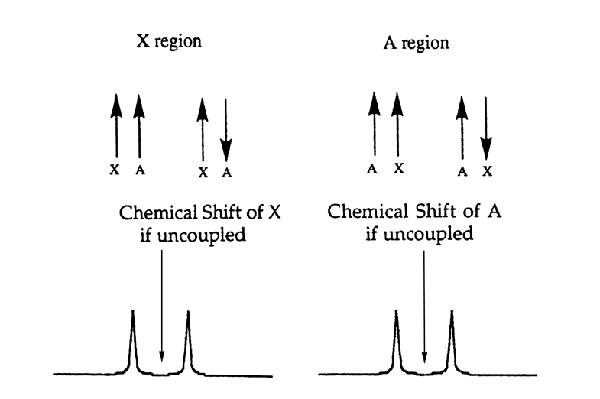
Figure 4. AX system and spectrum.
The more spins to which a group is coupled, the more complex the splitting patter for the signal of that group. The number of lines observed for a peak is called the multiplicity, M, which is a function of the number of equivalent nuclei to which the signal is coupled (n) and the spin (I) of the n nuclei:
M = 2nI + 1 (3)
If a group of spins is coupled to more than one set of nuclei, the rule above is followed for each set. For example, splitting of a group of protons by two inequivalent protons, would yield a doublet of doublets (Figure 5). If JAX and JAY were equal (this would be true if X and Y were in the same group), then the observed pattern would have three lines, with the central line having twice the intensity of the other two lines. For a group coupled to n equivalent nuclei, the number and intensity of lines follow the Pascal's triangle relationship (Figure 6).
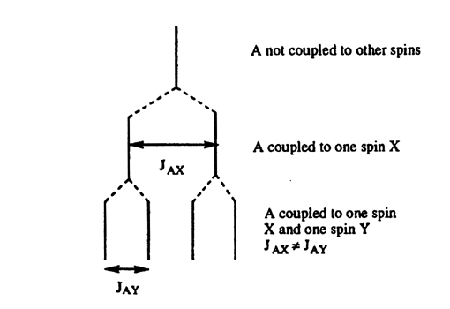
Figure 5. How a doublet of doublets arises.
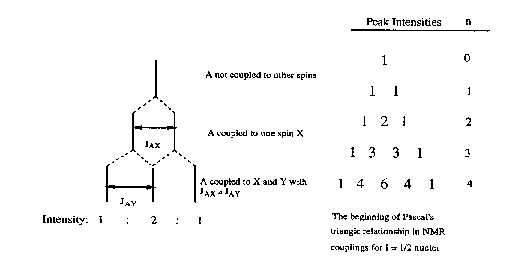
Figure 6. How a 1:2:1 triplet arises.
Reporting Coupling Constants
The magnitude of coupling is independent of field strength, so coupling constants are reported in Hz. Peak positions on NMR printouts are usually reported in ppm, so the coupling constants need to be converted into Hz. This can be done by multiplying the coupling in ppm by (probe frequency/ 10 6 ). Coupling constants are reported in the form XJAB, where A and B designate the type of nuclei involved in the coupling (i.e. 1H) and X is the number of bonds between the nuclei A and B.
Integration
As shown above, chemical shifts as well as the observed couplings provide information about the local environment of a given nucleus. Another useful aspect of NMR spectroscopy is that the intensity of the NMR signal is proportional to the number of spins giving rise to the signal. Integration of the peak areas in an NMR spectrum allows the relative intensity of all resonances for a given complex to be determined.
Quadrupolar Nuclei
Quadrupolar nuclei are nuclei with I > 1/2. For examples of quadrupolar nuclei, refer to Table 1. Quadrupolar nuclei give rise to 2I + 1 spin states, which can complicate spectra involving these nuclei. Another difference between quadrupolar nuclei and nuclei with I = 1/2 is that quadrupolar nuclei often undergo rapid relaxation, giving rise to broad lines. In some favorable cases, the spectra of quadrupolar nuclei can be observed. Additionally, coupling to quadrupolar nuclei can sometimes be observed in the spectra of I = 1/2 nuclei. For example, deuterium, the heavy isotope of hydrogen, has I = 1, giving rise to three spin states. If a group of spins is coupled to a single deuterium, the resonance will appear as a 1:1:1 triplet (Figure 7a). The three lines of this triplet are of equal intensity because the energy of the transition is being affected by three nearly equally populated spin states of a single nucleus (Figure 7b)

Figure 7. (a) How a 1:1:1 triplet arises and (b) the spin states of an I = 1 nucleus.
The Fourier Transform NMR Experiment
One way that NMR signals can be detected is by a continuous wave (CW) spectrometer. A constant radiofrequency is employed and the transitions between nuclear spin states are induced by sweeping the intensity of the magnetic field. The spectrum is obtained by monitoring the absorption of the radiofrequency as a function of field strength. CW NMR spectrometers were used for many years, but most NMR spectrometers now use the Fourier Transform NMR (FTNMR) technique. A block diagram of the FTNMR experiment is given in Figure 8. In the FTNMR experiment, an intense radiofrequency pulse of a few milliseconds is applied to the sample which excites all of the spins simultaneous. Monitoring all of the frequencies of radiation given off as the nuclei relax simultaneously, followed by a Fourier transformation, allows data to be collected much more rapidly than in a CW experiment.
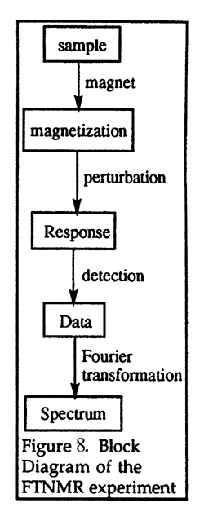
Figure 8. Block diagram of the FTNMR experiment.
Conventions used in FT-NMR Descriptions
The first convention to understand is how nuclear spins are represented in a coordinate system. The reference frame used is a coordinate system (Figure 9) in which the z direction is parallel to the static magnetic field, B 0.
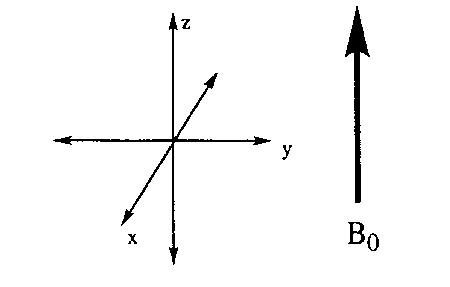
Figure 9. The coordinate system.
For a nucleus with I = 1/2 in a magnetic field, we know that the magnetic moment, mu, can align parallel or anti-parallel to the magnetic field. A torque is exerted by the magnetic field on the magnetic moments that is classically represented as a precession of the magnetic moments about the z axis like spinning tops. The precession takes place at the Larmor frequency (equation 4).
![]()
In contrast to the classical spinning top, precessing nuclear dipoles can only adopt specific angles with respect to the z-axis. For a nucleus with I = 1/2, the allowed angles are 54 degrees 44 minutes from the xy-plane (Figure 10).
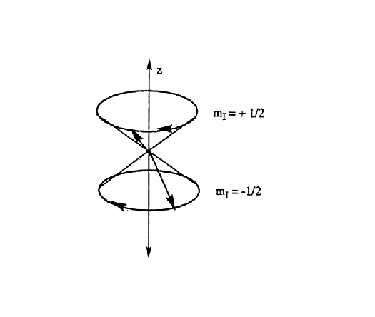
Figure 10. Precession of nuclei about the z-axis,
In a magnetic field, there are more spins aligned parallel to the magnetic field than antiparallel (see nuclear spin section), so the sum of all of the magnetic spin vectors yields the net magnetization, M0, which is aligned along the positive z-axis (Figure 11).
Figure 11. Net magnetization.
The next convention to understand is the rotating reference frame. It is confusing to think about a collection of magnetic vectors precessing about the z-axis at their Larmor frequencies. To simplify the picture, a rotating coordinate system is defined in which the x and y axes rotate about the z-axis at the Larmor frequency (Figure 12). Accordingly, any vector rotating at the Larmor frequency in the xy-plane of the stationary axis system is stationary in the xy-plane of the rotating reference frame.
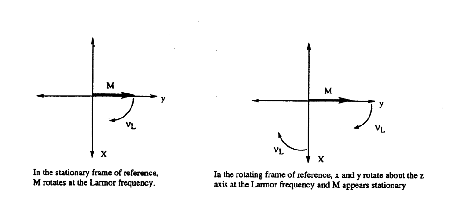
Figure 12. The rotating reference frame.
Affect of Radiofrequency on the Net Magnetization
As mentioned earlier, radiowaves of the proper energy can induce nuclear spin transitions in the sample. This is represented pictorially in Figure 13 (all figures are using the rotating reference frame). a radiofrequency pulse directed along the x-axis, designated as B1, exerts a torque on the net magnetization, M0, resulting in rotation in the yz-plane. In essence, M0 precesses about B1 for the duration of the B1 pulse in the same fashion as mu precesses about B0. The longer the duration of the pulse, the greater the angle of rotation of M0 in the yz-plane. When the radiofrequency field is turned off, the magnetization relaxes over time to its initial state.

Figure 13. 90 degree pulse and relaxation.
Relaxation
There are two types of relaxation in NMR called spin-lattice relaxation (represented by the time constant T1) and spin-spin relaxation (represented by the time constant T2 ). Spin-lattice relaxation is the return of the magnetization along the z-axis to its equilibrium value (Figure 14). The energy of the excited nuclei is transferred to the surroundings (called the lattice) as thermal energy hence the name spin-lattice relaxation.
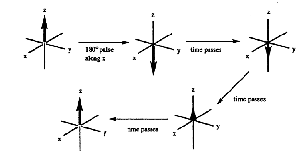
Figure 14. Spin-lattice (T1) relaxation.
Spin-spin relaxation is the loss of magnetization from the xy-plane (Figure 15). This process does not change the relative number of spins of each energy level, so no energy is released or absorbed by this process.
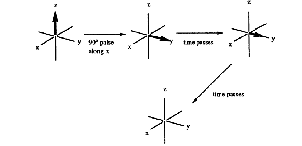
Figure 15. Spin-spin (T2) relaxation.
T1 and T2 time constants are indicative of the time required for relaxation (1/T 1 and 1/T2 are the rates of relaxation). T2 must be less than or equal to T1. If T2 were longer than T1, the magnetization along the z-axis could fully relax while there is still net magnetization in the xy-plane, an impossible result.
Detection of signal
Detection of NMR signals occurs in the xy-plane. In this discussion, we will assume the detector is aligned with the y-axis of the rotating reference frame. A component of the magnetization along the y direction is present when M 0 is rotated about the x-axis by a radiofrequency pulse (Figure 12). The projection of the magnetization along the y-axis decays exponentially over time, resulting in an exponential decay curve (Figure 15a). Such a curve is called a free induction decay or FID. This simple exponential decay is observed only if all of the spins of the system are precessing at the same frequency as the rotating reference frame, a rare situation. Usually, the frequency of the nuclei in the sample are shifted from the reference frequency. When a resonance frequency is shifted from the frame frequency, a sinusoidal pattern is introduced in the exponential decay. The frequency of the sine wave is equal to the difference (delta nu) in frequency between the precessional frequency of the nuclei being detected and the reference frequency. As shown below, this sine wave is observed because the y-axis is being probed by the detector while the magnetization vector is rotating in the xy-plane at a frequency delta nu. A pattern is produced, in which the difference in the peak maxima is 1/(delta nu). (Figure 15b). If the sample contains nuclei precessing at more than one frequency, the detected signal is a superposition of these different decay curves. Obviously, this situation yields a pattern that is not easily interpreted.
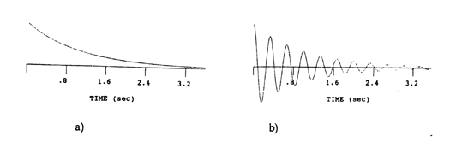
Figure 16. FID of one chemical shift at the reference frequency (a) and differing from the reference frequency by delta nu (b).
To deconvolute the complex time-domain behavior, a Fourier transformation (FT) is performed on the FID, which produces a spectrum in the frequency domain. In essence, the Fourier transformation takes the time dependence of each oscillation in the FID and converts it into a frequency. a distinct advantage of the FTNMR experiment is that FIDs from many pulses can be added together and then transformed. This yields a better signal to noise ration and allows spectra to be obtained with very small amounts of sample.
This page was adapted from a lab manual written by Michael R. Jordan and Cynthia K. Schauer at the University
of North Carolina at Chapel Hill. This page is maintained by Michael Jordan.